It takes a remarkable amount of processing to keep track of where things are, even in a simplified virtual reality.
While working on a recent simulator project, we implemented several algorithms that may have application in other programming domains. Our purpose was to determine a helicopter's height above terrain. That is, given the helicopter's x-y-z position in the simulator's 3-D problem-world, and the terrain of that problem world represented by a collection of x-y-z points, these algorithms would find the distance between the helicopter and a point on the terrain directly below. In the course of implementation, we developed methods for solving the following problems:
- determine efficiently if two line segments intersect
- determine whether a point lies between, or outside of, a pair of diverging vectors
- connect a group of randomly scattered points on a plane so as to tile that plane with near-regular triangles
Of course, for the purposes of the simulator project the crucial thing to determine was height above terrain. It goes without saying that if the helicopter's height ever went below the height-of-terrain (HOT), it would experience "inadvertent ground contact" — something we'd rather avoid.
The definition points represent the tops of hills, certain landmarks and NAVAIDS, coastlines, and the problem-world boundaries. There are several ways to model the terrain that lies between these points. One way is to tile the problem-world with uniform triangles. Using uniform triangles brings with it the advantage of a simple formula, given the helicopter's position, for determining which triangle the helicopter is over. But this method requires a laborious initial adjustment of the triangles' vertices, to force the modeled surface to conform to the terrain points, and to preserve altitude continuity of adjacent triangles.
Another way to model the terrain is to triangulate it using the definition points themselves as vertices. If we take this approach we need a good triangulation algorithm. Also, once the simulation is running, we need a good search algorithm to determine which triangle the helicopter is over. Once the triangle is found it is a simple matter to compute the height of terrain, given the three vertices of the triangle and the 2-D position of the helicopter within the triangle.
I describe this latter method in the article that follows. A small warning: this method involves quite a bit of 2-D vector analysis. To simplify the equations to make them suitable for coding in C++, I had to do a lot of algebra as well. (A good symbolic manipulation program, such as Mathematica or Maple, is quite helpful here. I used a program called Theorist, which I fear is no longer available.) Fortunately, you should be able to skip most of this math (if you wish) and still understand what's going on with the underlying algorithm.
Triangulation
First, note that triangulation is a 2-D problem, even though the problem-world is a 3-D place. The triangulation algorithm uses only the 2-D coordinates of the helicopter over the 2-D triangulation of the terrain. The altitudes of the vertices and of the helicopter come into play only later, when the simulation is running, because that is when height above terrain is calculated.
The problem-world is laid out with x and y axes on the ground and the z-axis representing altitude. Thus, the triangulation algorithm uses only the x and y coordinates and ignores z. A sample problem-world appears in Figure 1. This figure shows the problem-world boundary having four vertices, with five terrain definition points inside.
As a first cut at triangulation, consider the following Nlog(N) algorithm: a) select one of the vertices and draw as many lines as possible from this point to the other vertices (including the boundary points). b) Move to another vertex and draw as many lines as possible to the other vertices without intersecting the lines already drawn. Proceed in this manner through the remaining vertices until the triangulation is complete. The resulting triangulation of the problem-world in Figure 1 appears in Figure 2. In this case the triangulation algorithm began at the lower-right hand corner. Starting at this corner caused a lot of segments to be connected to the first vertex, thus forming lots of long skinny triangles
Figure 3 shows the output of a different triangulation algorithm. Unfortunately, this new algorithm has a complexity of N2, so it generally takes longer to complete. However, the resulting triangulation exhibits none of the long, narrow triangles, which is an important consideration when computing altitudes. Suppose, for instance, that this problem-world represented an island, with the four corner vertices at sea level, and the interior points representing mountain peaks. The Nlog(N) algorithm actually connects the lower-right vertex with the upper-left vertex, producing a sea-level segment running right through the center of the island. That makes the Nlog(N) algorithm undesirable for this sort of simulation.
This N2 triangulation is what I call the optimal triangulation. The optimal triangulation algorithm starts by creating a list of all possible segments between all possible pairs of vertices. This list of segments is then sorted by length, shortest to longest. Next, the procedure selects the shortest segment from the list and admits it automatically as part of the triangulation. Then the next segment in the list is examined, and if it doesn't intersect any segment already in the triangulation, it is added to the triangulation. The algorithm proceeds in this manner, selecting elements from the sorted list from shortest to longest. It adds the selected element to the triangulation if it doesn't intersect any other segment already in the triangulation. (The segment can share an endpoint with another, however.)
Clearly, most of the longer segments won't make it into the triangulation. The algorithm is complete when the sorted list has been exhausted [1] .
In this sort of topology, the number of segments in the triangulation will be:
number of segments = 3 * (total number of vertices - 1) - number of boundary verticesAlso:
number of triangles = number of segments - total number of vertices + 1So the differences between the optimal triangulation and the Nlog(N) triangulation are just in the shape and disbursement of the triangles. Both produce the same number of segments and the same number of triangles given the same set of vertices. The optimal triangulation will have the shortest sum of segment lengths of any triangulation.
Detecting Intersections
The two triangulation algorithms do have at least one thing in common: they need a way to determine if two segments intersect. In both algorithms, a candidate segment is tested for intersection with all the segments already in the triangulation. Since there are a large number of such tests, the test for intersection must be fast.
The intersection test relies upon a couple of sub-tests. In this section I describe the sub-tests first, and build upon each to reach the final intersection test.
The starting point for building the intersection test is the simple dot product. Given a vector u = (x1, y1) and v = (x2, y2), the dot product is:
u * v = x1*x2 + y1*y2Using the dot product, it's easy to surmise the angle, q, between two vectors, from the relationship:
cos q = u * v ------ |u||v|where |u| represents the magnitude of the vector u,
Fortunately, in this application it is not necessary to actually solve for q, which would involve expensive calculation; it is enough to know whether q is acute or obtuse. (An angle is acute if its magnitude is less than or equal to 90 degrees; otherwise it is obtuse.) To find out if q is acute or obtuse, we need only know the sign of cos q. And the sign of cos q is far easier to calculate than q; since the magnitudes |u| and |v| are always positive, the sign can be derived from the above equation as:
sgn(cos q) = sgn(u * v)sgn(u * v) will be positive if the angle between the two vectors is acute; and it will be negative if the angle is obtuse.
This first sub-test isn't quite what we need. The next sub-test to develop (building upon the acuteness test) is one that determines whether one vector lies on the "left side" or "right side" of another. That is, given a vector u and v emanating from the same point
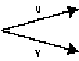
is vector u on the left or right side of v? (More precisely, is u counterclockwise, or clockwise from v? In this article, u will be considered "left" if it is counterclockwise from v, and vice versa.)
To answer this question, construct a vector perpendicular to u, and take the dot product of this new vector with v. The side that u lies on with respect to v is indicated by the sign of that dot product. Given
u = (x1, y1)its perpendicular is
perp(u) = (-y1, x1)and the side u is on is given by
sgn(perp(u) * v) = sgn(-y1*x2 + x1*y2)Specifically, if the sign of the above expression is negative, u is on the left of v; if it's positive u is on the right of v.
It may not be apparent how the first test, for acute angles, plays a part in determining sides. But if you examine the equation immediately above, you'll see that it's really testing whether the perpendicular of u makes an acute or obtuse angle with vector v. If the perpendicular makes an obtuse angle with v, u is on v's left; if the perpendicular makes an acute angle with v, u is on v's right.
Now I show how to use this test to determine if two line segments intersect. Figure 4 shows two line segments, S1 and S2. The segments are determined by their endpoints; the endpoints for S1 are a0 and a1; S2's endpoints are b0 and b1. The goal here is to first determine mathematically if S2 crosses the line containing S1 (shown as a dotted line in Figure 4) . To determine this, construct two vectors from an endpoint of S1 to the endpoints of S2. These are the vectors (a0-b0) and (a0-b1) in Figure 4. If S1 lies between these two vectors, then S2 crosses S1's containing line.
S1 lies between these two vectors if it lies on opposite sides of each. So to find out if it's between, construct a vector, (a0-a1), along the segment S1, and apply the "sideness" tests from the previous section. Thus, the test for betweeness is:
test1 = sgn(perp((a0-a1)) * (a0-b0) * perp((a0-a1)) * (a0-b1))If test1 is negative, then S2 crosses the line containing S1.
This same technique can be used to determine if S1 crosses the line containing S2:
test2 = sgn(perp((b0-b1)) * (b0-a0) * perp((b0-b1)) * (b0-a1)If both test1 and test2 are negative, then both S1 and S2 cross each others' containing lines. If S1 and S2 both cross each other's containing lines, S1 and S2 must intersect.
The code for the intersect function appears in Listing 1. This code implements a vector as a C++ class, along with member functions to calculate the dot product and perpendicular of a vector. If we were to write out these equations all the way down to their plane coordinates, it would be very easy to mess up a sign. (Note: In the code listing, vector is a construct with two endpoints, so it corresponds to a line segment as discussed in this text. A segment has the two endpoints and a length field, used for sorting.)
The intersect function considers two segments intersecting if one of the following is true:
- both test1 and test2 are less than zero
- one of the tests is less than zero and one of them equals zero
If either of test1 or test2 is greater than zero, the intersect function returns a false indication (i.e. the vectors don't intersect).
The above scenarios cover every case except the one in which both tests are zero. When both tests are zero, the algorithm must distinguish between one of the following possibilities:
- the two segments share only an endpoint and are not parallel (that is, they do not lie along the same line)
- the two segments are parallel and overlap
- the two segments are parallel and share only one endpoint
- the two segments are parallel but are completely separated
The test for parallel segments is:
perp((a0-a1)) * ((b0-b1)) != 0If this dot product is non-zero, then the segments are not parallel and share only a common endpoint. They are not considered to intersect. If this dot product is zero then the segments are parallel, and they lie along the same line. In this case, a decision matrix tests whether the segments overlap, share an endpoint, or are separate. This decision matrix is just a bunch of if statements contained in the function between (Listing 2) . Given two points, between determines whether a third point lies between them. between deals only with the points' projection on the x-y plane; it does not take into account their z-coordinate.
Joining the Segments
The create_triangulation function (Listing 3) is where the triangulation is actually created. This function starts with a_array, which contains all the definition points of the problem-world. The function first creates all possible segments from all possible pairs of points in a_array. This set of all possible segments is placed in b_array. (I apologize for the lack of descriptive names for these arrays.) After that, the b_array is shell-sorted from shortest to longest segments. The c_array will contain the triangulation. The algorithm sequences through the b_array and adds the segments to the c_array only if they don't intersect the segments already in c_array.
The c_array will contain all the segments of the finished triangulation, with the segments already in ascending order of length. But when the simulation runs, it must search for the triangle the helicopter is over, and the c_array provides no systematic way of determining how the segments connect together to form triangles. Enter the d_array. For every segment added to the triangulation in c_array, that segment is added to the d_array, and then it is added to the d_array again with its endpoints switched. So every segment in the triangulation is added to the d_array twice.
When this process is complete, the d_array is sorted, only not by length. The sort routine places all segments with the same first endpoint together. Then all segments that share the same first endpoint are sorted in a counter-clockwise order around the common endpoint. That is, the larger the angle a segment makes with the x-axis, the further down the list it will end up. This second sort explains why each segment appears twice in d_array. Each segment must reside in an ordered list corresponding to each of its endpoints.
The workhorse for this sort routine is the vector operator< function (Listing 4) . This function determines if there is a common first endpoint then calls the angle function to determine the angle of the segment with respect to an x axis unit vector. The angle function simply uses the dot product definition to calcluate the angle, then some logic to determine which quadrant the segment is in.
The next step is to create the conjugate_idx array. Given a vertex and a segment connected to that vertex, the conjugate_idx array contains the index in d_array where the other endpoint of the segment can be found. In other words, the conjugate_idx array contains the index of where a segment's duplicate (with endpoints switched) is in the d_array.
The triangulation now contains enough information for the search algorithm, which will execute when the simulation runs. The search algorithm will use only the d_array and the conjugate_idx array to search the triangulation. So at the end of the triangulation process only these two arrays are saved to disk for use at run time. Arrays a_array, b_array, and c_array are discarded.
It should be noted that the part of the triangulation algorithm that uses the most CPU time is the sorting of the b_array and the sorting of the d_array.
The Search Algorithm
The search algorithm runs when the simulation runs, after triangulation is complete. The search algorithm figures out which triangle the helicopter is flying over. The search algorithm begins by choosing any vertex. The d_array provides a list of the segments connected to that vertex. Note that if these segments are extended from their free endpoints, they divide the problem-world into wedges, like a pie.
The search algorithm then determines which wedge the helicopter is over. That wedge is made up of two segments (which are adjacent in the d_array because of the way it is sorted). After it has identified the two segments containing the helicopter, the algorithm chooses the "first" of these two segments and uses the conjugate_idx array to find its other endpoint. The algorithm then moves to that new vertex and repeats the entire process.
It doesn't take long before the wedges the helicopter is over also make up the triangle that it is over. Specifically, if the algorithm is iterated three times and returns to the same point, it has traversed the triangle containing the helicopter.
That is the basic algorithm, but it needs some modifications for the run-time application. It is clear that when the search algorithm is first starting up, it must traverse quite a few of the vertices before it comes to the three vertices of the correct triangle. Also, when the helicopter passes out of the triangle, the algorithm may pass through a few other vertices before settling down on the new triangle. Once the triangle has been determined, then as long as the helicopter stays in the triangle, the search routine will just cycle through that triangle's vertices. As a result, the algorithm requires different amounts of time in different situations. But some systems absolutely need a deterministic algorithm.
To provide a deterministic algorithm the code just cycles through two vertices each time the search is called. (Actually in the listing here, it just does it once.) The code might take a few calls at the beginning to get to the enclosing triangle, but after that, just checking two vertices and the wedges from those two vertices is sufficient to see if the helicopter is still in the triangle.
There is a special case which occurs on the problem-world's boundary points. As the pairs of segments are read out of d_array, the two segments that are boundary segments for a boundary vertex will form a wedge that spans the whole problem-world. This condition is easily detected with the angle function, which will return an angle larger than pi for this condition.
In or Out?
The heart of the search algorithm is the part that determines when a point is within a wedge created by two segments. To understand how this operation works, begin by simply thinking of these segments as vectors. As long as the two vectors are not parallel they will span the 2-dimensional plane, and every point of the plane can be expressed as a linear combination of the two vectors. In math linguo, if u and v are the two vectors, then any point h of the plane can be expressed as:
Au + Bv = h.Where A and B are real numbers. If we draw a line through u and a line through v (so that the lines contain u and v), they will divide the plane into four (not necessarily equal) quadrants. Any point lying in the first quadrant will be a linear combination of u and v with positive coefficients. In fact, the quadrant of any point on the plane can be determined by looking at the signs of the coefficients of the linear combination. To see if the helicopter is in the wedge defined by the two segments, compute the coefficients of the linear decomposition. If both coefficients are positive then the helicopter is in the wedge.
Let Su and Sv represent the two segments, and H represent the position of the helicopter. If Su has endpoints x0,y0 and x1,y1 and Sv has endpoints x0,y0 and x2,y2 and H is the point xh,yh, then the vectors corresponding to the Su, Sv, and H respectively are:
u = (x1 - x0, y1 - y0) v = (x2 - x0, y2 - y0) h = (xh - x0, yh - y0)Since h is a linear combination of u and v, h = Au + Bv, and solving for A and B yields:
A = ((xh - x0)(y2 - y0) - (x2 - x0)(yh - y0)) ---------------------- ((x1 - x0)(y2 - y0) - (x2 - x0)(y1 - y0)) B = ((x1 - x0)(yh - y0) - (xh - x0)(y1 - y0)) -------------------- ((x1 - x0)(y2 - y0) - (x2 - x0)(y1 - y0))and if both A and B are positive, then the helicopter is in the wedge.
Search Algorithm Code
It is the ordering of segments in d_array that makes the search algorithm work. Recall that segments residing in the d_array are grouped together by common vertex, and then sorted within that group according to segment angle.
In the code for the search algorithm, the postfix function (Listing 5) relies upon this sort order to find the adjacent segment when the index of the current segment is passed to it. Most of the time postfix will just return the next index into d_array. But this routine must "wrap around" the vertex when the current segment is the last one connected to the vertex; in this case the adjacent segment is the first one connected to the vertex.
The find_triangle routine (Listing 6) starts with either the segment it left off with the previous time, or with the zero index the first time it is called. The next segment from d_array is found and then it is checked to see if the pair of segments are boundary segments. Once that is done, the position of the helicopter is checked to see if it is in the wedge spanned by the two segments.
The routine gets the new segment and uses the conjugate index to find its other endpoint; the routine is now set for the next iteration. The routine also keeps track of the previous two vertices that it visited. When the current vertex is the same as the vertex found three iterations previous, then the triangle containing the helicopter has been found.
Finding Height of Terrain
The remaining functions described in this article are relatively high-level and don't need to be shown here. (All the functions are available on the CUJ ftp site — see p. 3.) do_it calls find_triangle and after a triangle has been found, computes the height of terrain directly beneath the helicopter. Given the three points of the triangle and position of the helicopter:
p1 = (x1, y1, z1) p2 = (x2, y2, z2) p3 = (x3, y3, z3) and ph = (xh, yh, zh)If the equation of the plane containing the triangle is:
a*x + b*y + c*z = dthen
a = (y1 - y2)(z1 - z3) - (y1 - y3)(z1 - z2) b = (x1 - x3)(z1 - z2) - (x1 - x2)(z1 - z3) c = (x1 - x2)(y1 - y3) - (x1 - x3)(y1 - y2)and d is
d = a*x1 + b*y1 + c*z1Finally, the height of the point on the triangle under the helicopter is given by:
height = (d - a*xh - b*yh) / cThe triangulation program calls the give_vertex to add each definition point of the problem world. Next create_triangulation is called to generate the triangulation. Then the save_triangulation routine saves the triangulation data to the disk.
When the simulation runs, it calls load_triangulation first to load the triangulation data from disk. After calling give_position to specify the position of the helicopter (or whatever the point in question is), the do_it routine can be called to search for the triangle containing the position.
And It Works
This code was originally written in Ada for the SH-2G helicopter simulator for the Navy. (The code is now in public domain.) It was ported to C++; the code accompanying this article runs under Borland C++ v4.5. The code also includes lines to generate a graphical display of the process using Borland's BGI libraries. On my PC, these routines can handle a problem-world defined with up to 60 points. The Ada implementation generated a problem world with over 300 definition points on a Sun Sparc box in about 7 minutes. The run-time component was run on embedded Force 68030 boards, so there was a definite separation of triangulation creation and triangulation search. o
Notes
[1] Or a counting argument can be implemented to compute the number of segments in a completed triangulation, and stop the algorithm when that number of segments has been added to the triangulation.
J. David Wendel has a B.S. in math from Brigham Young University and an M.S. in math from the University of Utah. He has spent seven years as an embedded systems programmer. Four of those years were at Eyring Corporation, coding in Ada for the Navy's SH-2g helicopter simulator. The last three years have been at Raytheon Aircraft Montek Company, coding GPS aircraft landing systems for the FAA and the Navy in C/C++. He can be reached at dwendel@montek.com.